%chebyshev HPF
%for specification
clear all;
alphap=input('pass band attenuation?=');
alphas=input('stop band attenuation in db?=');
wp=input('pass band frequency in rad?=');
ws=input('stop band frequency in rad?=');
%to find cuttoff freq and order of filter
[n,wn]=cheb1ord(wp/pi,ws/pi,alphap,alphas);
%system function of filter above expression
[b,a]=cheby1(n,alphap,wn,'high');
w=0:.01:pi;
[h,ph]=freqz(b,a,w);
m=abs(h);
an=angle(h);
subplot(221);
%plot the graph
plot(ph/pi,m);
grid;
ylabel('gain in db');
xlabel('normalisd frequency');
subplot(212);
plot(ph/pi,an);
grid;
ylabel('phase in rad');
xlabel('normalised frequency');
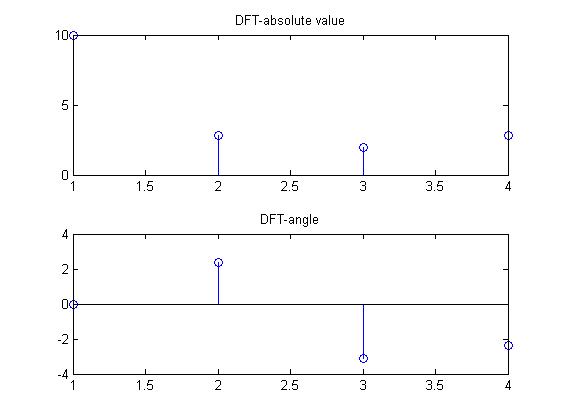
OUTPUT WAVEFORM